Таджикский технический Университет имени академика М.С.Осими

Аннотация

В данной работе был рассмотрена математическая модель насосного агрегата с частотным преобразователем частоты.

• Математическая модель системы электропривода ПЧ-АД.

На рис.1.1 приведена, математическая модели с расчётными параметрами рассматриваемой системы электропривода ПЧ-АД, без раскрытия математической модели АД.

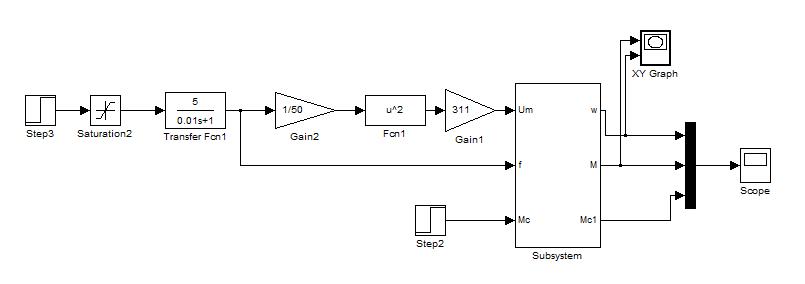
Рисунок 1.1. Математическая модель системы электропривода ПЧ-АД.

На рисунок 1.2. приведена, математическая модель асинхронного двигатель с указанием всех расчётных коэффициентов и регулируемых, входных и выходных координат, для подсоединения к математической модели общей системы электропривода ПЧ-АД.

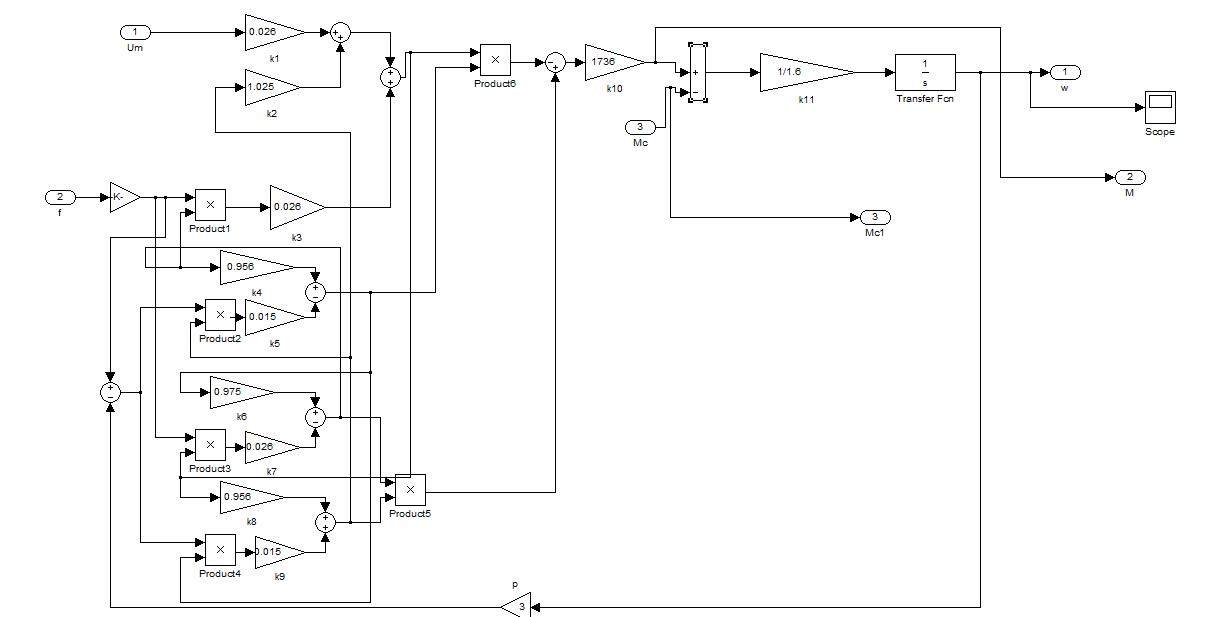
Рисунок 1.2. Математическая модель асинхронного двигатель.

Общая математическая модель системы электропривода ПЧ-АД позволяет провести исследование проходных процессов для различных режимов работы исследуемого электропривода.

В данной математической модели необходимо учесть момент сопротивления насосы, для этого я предлагаю применить следующую структурную схему и выражение учитывающее изменение момента от скорости

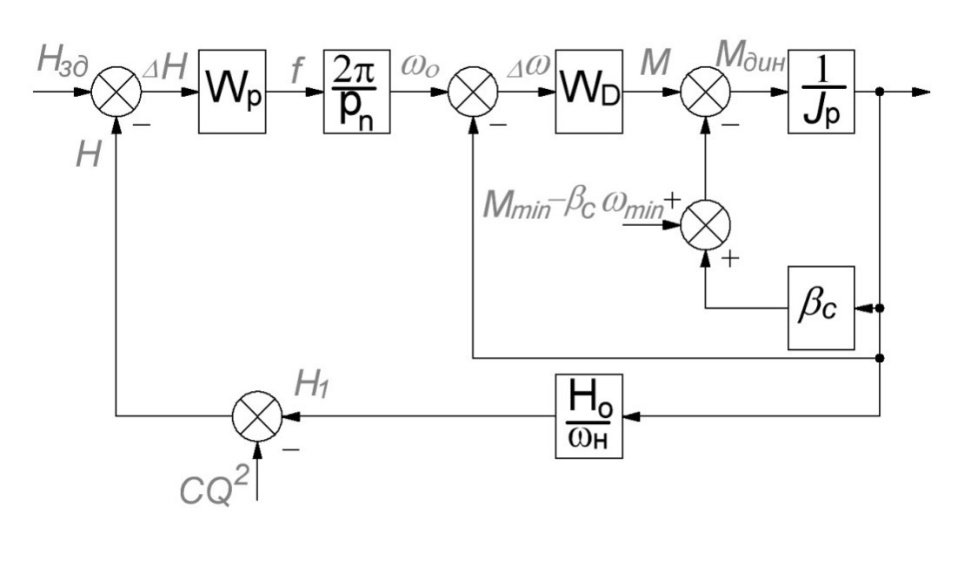
Рисунок 1.3.  -  Линеаризованная структурная схема электропривода при стабилизации напора в рабочем диапазоне

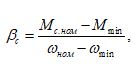
β_с – модуль жесткости механической характеристики турбомеханизма;

Произведем расчёт расчет параметров математической модели объекта управления.

1.2. Расчёт параметров схемы замещения асинхронной машины.

Для расчета выбран асинхронный двигатель с короткозамкнутым ротором приведены выше:

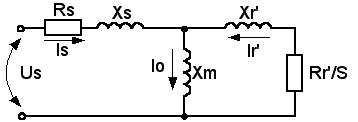
Рис.1.4. Г-образная схема замещения АД.

1.3. Расчет параметров уравнений обобщенной асинхронной машины.

1.4.  Расчет параметров преобразователя частоты

Передаточная функция преобразователя частоты

1.5. Исследование динамики системы управления насосной установки на Matlab

Для отображения переходных процессов на диаграммах, произведём моделирование пуска двигателя насосов установки и разгона его до номинальной скорости (ω_ном= 314рад/с; H_зд= H _ном = 27) без обратного значения давления. При достижении номинальной скорости и требуемой высоты напора, в первый момент времени изменим значение расхода воздуха подадим сигал ступенчатым образом блоком “step”. Данное манипулирование значением расхода воздуха позволит проанализировать полученные данные и сделать необходимые выводы. Графики переходных процессов представлены на следующих рисунках:

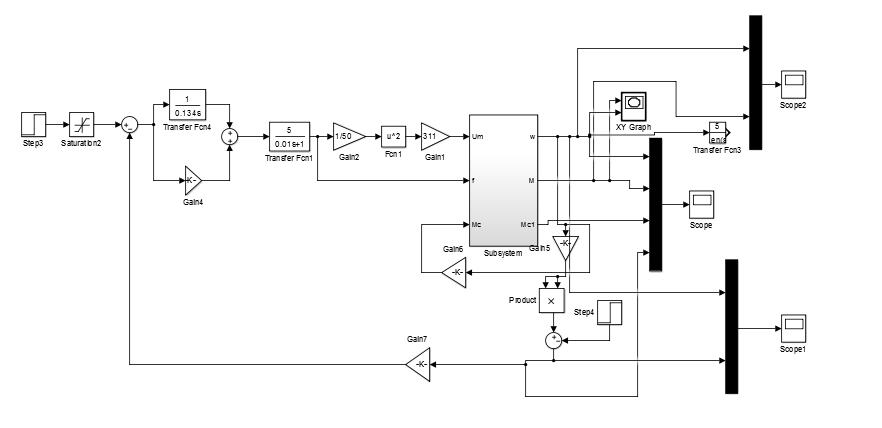
Рисунок 1.5. Модель автоматизированного электропривода при частотном управлении

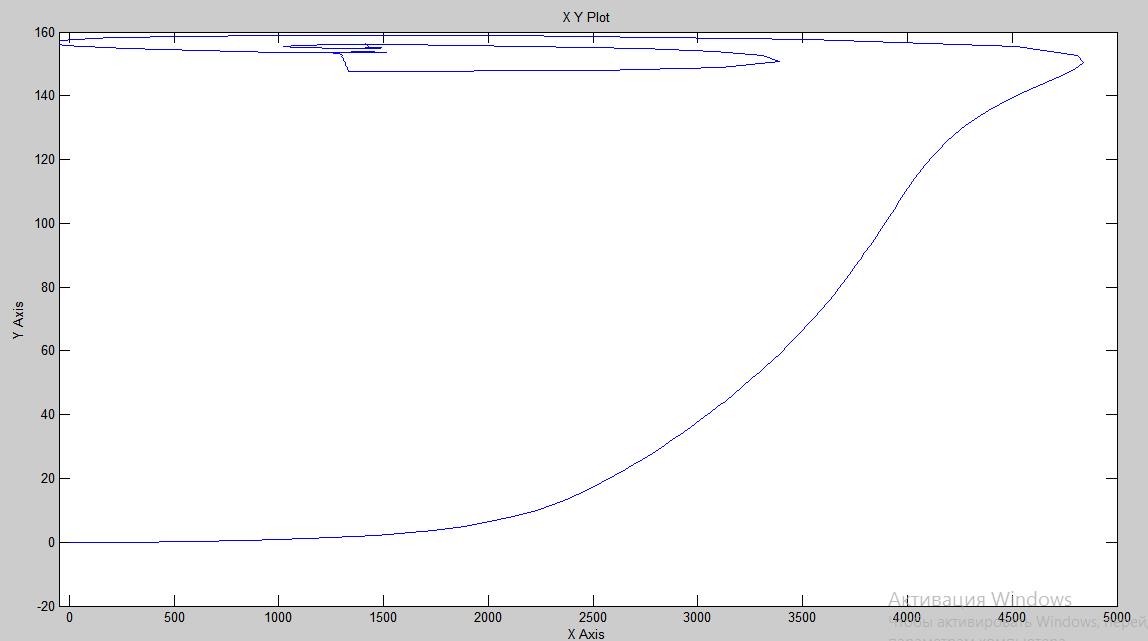
Рис.1.6. Фазовая характеристика в режиме пуска на номинальную скорость

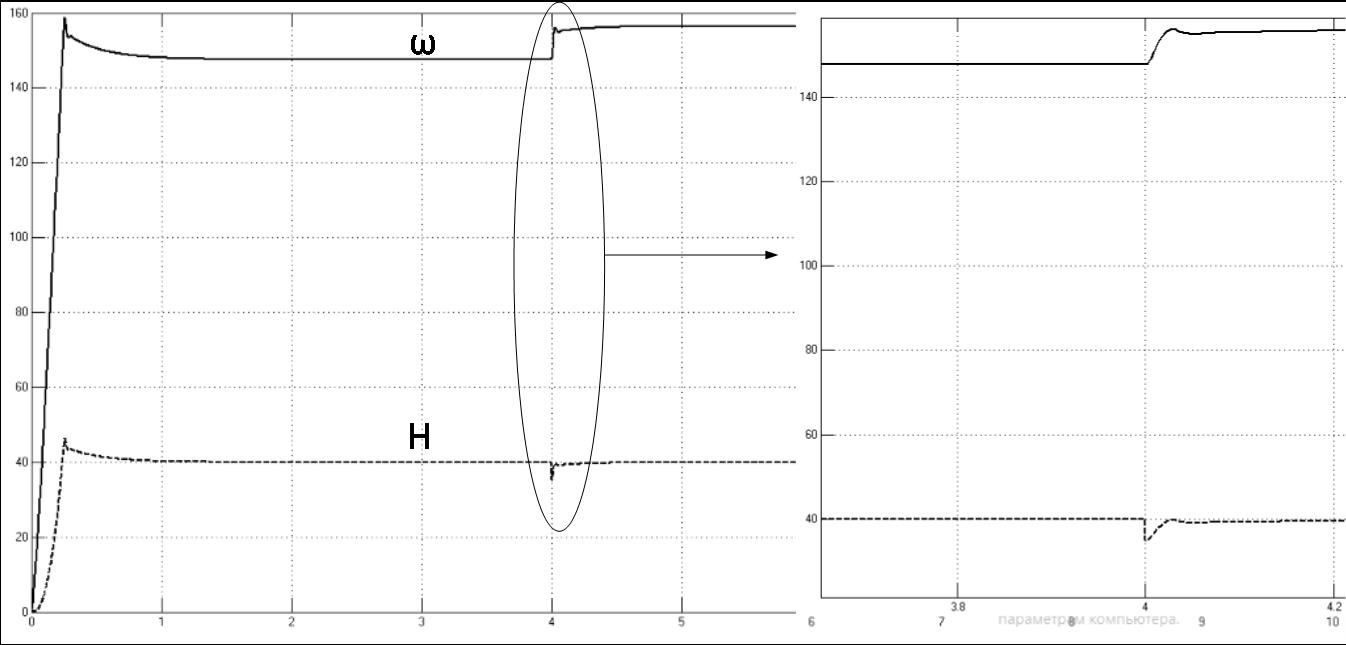
Рисунок 1.7. Переходные процессы изменения скорости двигателя и давления при увеличении расхода воды.

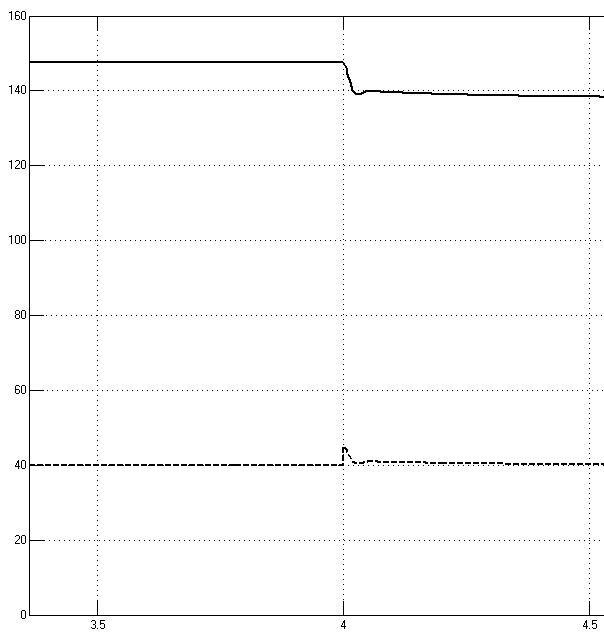
Рисунок 1.8. Переходные процессы изменения скорости двигателя и давления при уменьшении расхода воды

В результате компьютерного имитационного моделирования были получены переходные процессы автоматизированного электропривода насосов для подачи воды.

Определение показателей качества системы будет определяться такими параметрами, как величина регулирования, время регулирования и числом колебаний исходной величины до установившегося значения за время переходного процесса.

Для оценки перерегулирования нашей системы проанализируем график переходного процесса зависимости угловой скорости от времени. Как можно убедиться, перерегулирование будет очень низким рисунок 1.8. Таким образом колебательность системы можно принять близкой к нулю, так как значения не превосходят 5% от установившегося режима.

Быстродействие, определяемое временем достижения системой значения установившегося состояния, составляет порядка 0,3 секунд.

Литература

1. Водоснабжение. Учебник для вузов. - Н.Н. Абрамов, Москва, Стройиздат, 1974 г.
2. Белозоров Н.П., Луговской М.В.Расчет систем водоснабжения с применением вычислительной техники. М.: Колос, 1973 г.
3. Ильин В.Г. Расчет совместной работы насосов, водопроводных сетей и резервуаров. // Киев, Госстройиздат УССР, 1963 г.
4. Лезнов Б.С.Энергосбережение и регулируемый привод в насосных и воздуходувных установках. М.: Энергоатомиздат, 2006 г.
5. Лезнов Б.С.Характеристики разветвлённых трубопроводов с промежуточными отборами воды // Водоснабжение и санитарная техника. 2007,No 12.
6. Карелин В.Я., Минаев А.В.Насосы и насосные станции. М.: Стройиздат, 1986 г.

Диёров Р.Х. Давлатов А.А.

ТТУ имени академика М.С. Осими, г. Душанбе.